[10000印刷√] 数学 階級 値 683847-中1 数学階級値

平均値と階級値について 苦手な数学を簡単に

 中学数学の質問です。統計が苦手で今でもわからないので教えてください。・度数分布表では階級を「 以上 未満」と表しますが、階級値(階級の中央値)を求めるのに の値をつかうのはなぜでしょうか。 はその階級では「未満」なので含まれな平均 = (階級値×度数)の合計 ÷ 度数の合計 なので {05×615x25×335 (10x)45×1}÷=16 (315xx45)÷=16 (2x50)÷=16 2x50=32 2x = 18 x = 9 y=10x なので y=1 4 表はあるクラスの生徒の通学時間をまとめたものである。 このクラスの通学時間の平均値は22分である。 x,yの値を求めよ。 x,y以外の人数の合計が 7612=16である。 つまりxとyの合計が 30

中1 数学階級値

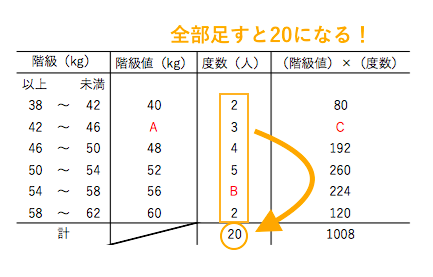
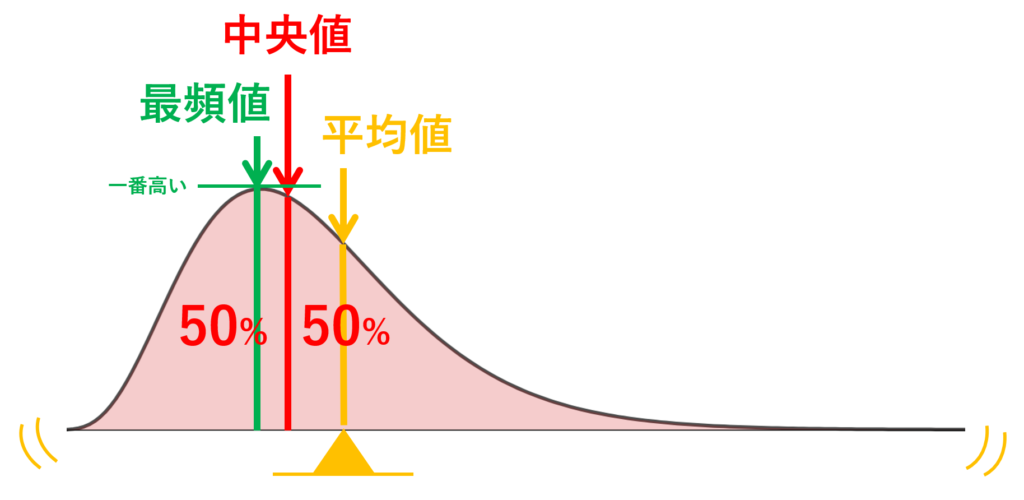
中1 数学階級値-各階級の階級値を出す。 各階級で階級値 × 度数 を計算する ②の結果をすべて加える。 ③の結果を度数の合計で割る。 平均値 = (階級値 × 度数)の総和 度数の合計 例 生徒人の垂直とびの記録 平均値 1170÷=585 中央値 (メジアン) 資料の値を大きさの順に並べた時の中央の値を 中央値 (メジアン) という。 例 生徒25人の身長の中央値は低い方から13番目の人の値となる (高い方から数えても13番度数の最も大きい階級の階級値としての仮変数を 0 にすることの長所は，大きな度数でも 0 を掛けることになって，計算が省略できるからです．（上記の計算中の 0×7 ） 度数分布表の中央付近で，仮変数 0 にすると大きい方も小さい方も ±2 のように小さな整数値になって，計算が楽になるから

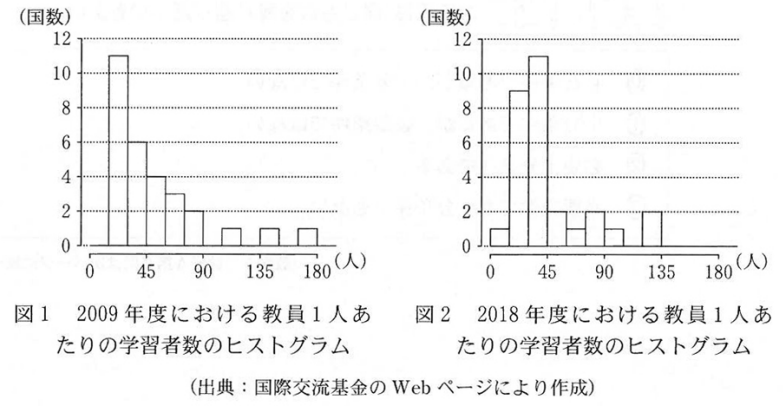
共通テスト 数学i 数学a 22年度 第2問 2 解説 なかけんの数学ノート

これについて、以下の問いに答えなさい。 1 男女それぞれの中央値（メジアン）を求めなさい。 2 男女それぞれの平均値を小数第二位まで求めなさい。 男子 ⇒ （39＋40＋43＋44＋45＋48＋52）÷7＝44．428 右の表は、あるクラスの生徒35人の数学のテス進研ゼミからの回答 度数分布表から平均値を求めるときは,その階級の真ん中の値（階級値）を使います。 つまり,50点以上60点未満の4人の点数はすべて55点とみなすのです。 この階級値を使うと,「55点が4人,65点が2人,75点が2人」ということになり,平均値は「階級値」というのは、その 「階級の真ん中の値」 のことなんだ。 具体的に見た方がイメージしやすいから、実際に例題を解いて確認してみよう。 この授業の先生 今川 和哉 先生 どんなに数学がニガテな生徒でも「これだけ身につければ解ける」という超重要ポイントを、 中学生が覚えやすいフレーズとビジュアルで整理。 難解に思える高校数学も、優しく丁寧な語り口で指導。 「最頻値」と「階

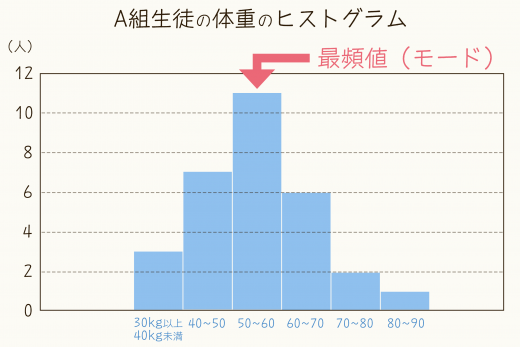
最頻値（モード）とは、 データの中でもっとも度数が大きい階級の値 です。 つまり、 登場回数が1番多いデータの値 のことです。 本記事では、 最頻値の意味と求め方について解説 します。 最頻値（モード）は代表値のなかでも簡単な用語なのでしっかり覚えていきましょう！階級（かいきゅう） 社会階級 身分・職業・学歴・財産などにより形成される社会集団。 階級闘争、上流階級、労働者階級など。;ランク）は、行列の最も基本的な特性数 (characteristic) の一つで、その行列が表す線型方程式系および線型変換がどのくらい「非退化」であるかを示すものである。 行列の階数を定義する方法は同値なものがいくつもある。

中1 数学階級値のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

データの平均値 中央値 最頻値の定義と解釈 数学の景色	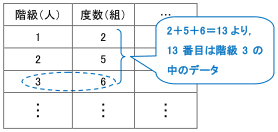データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	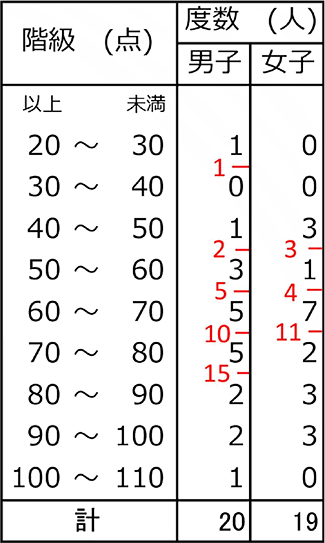データの平均値 中央値 最頻値の定義と解釈 数学の景色	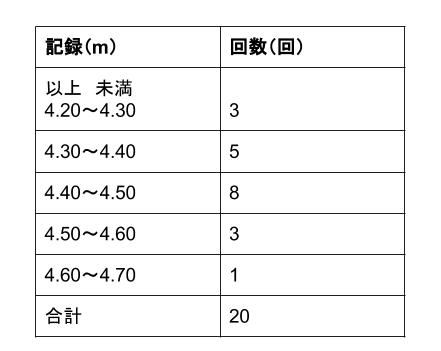データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	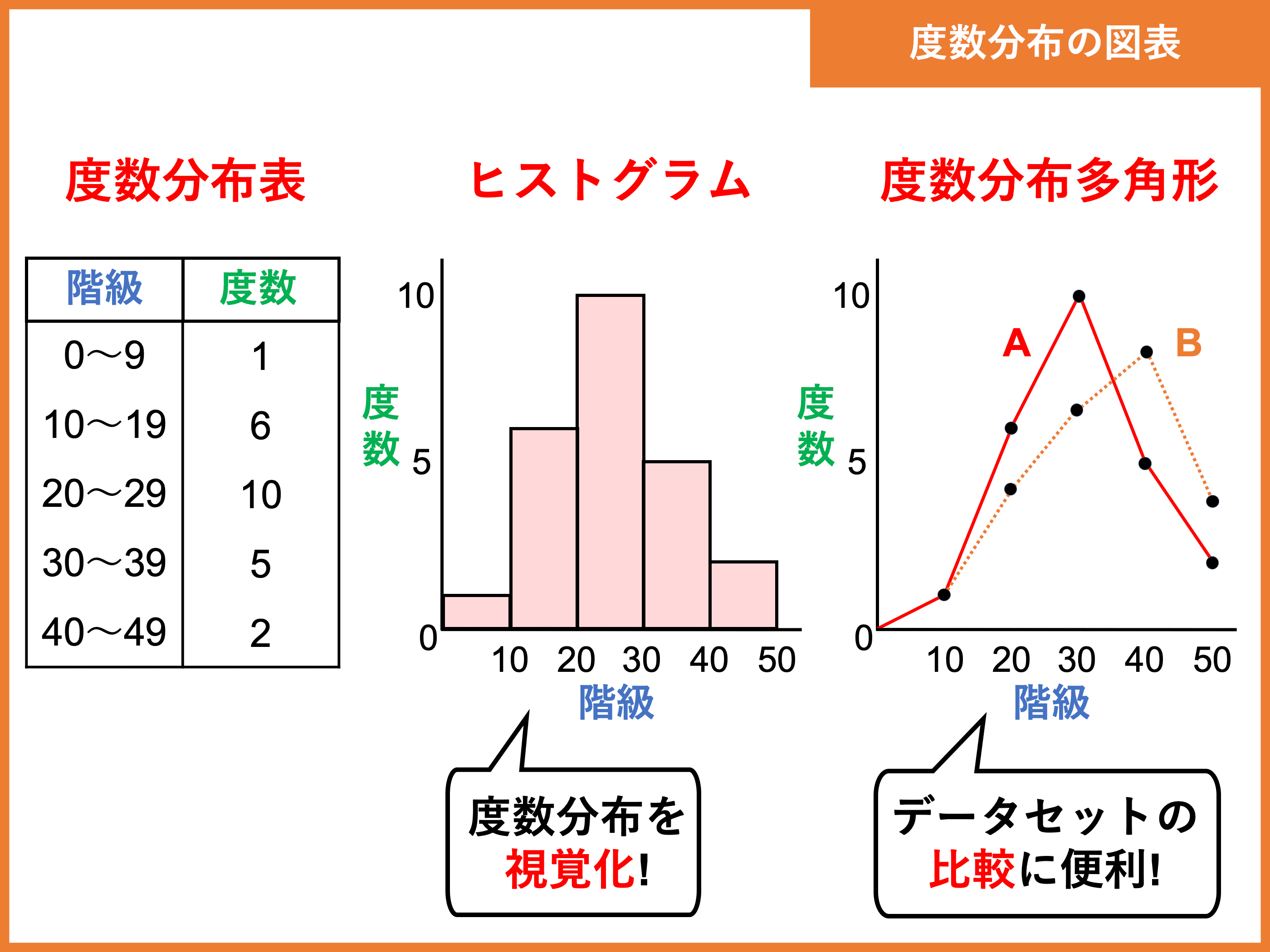データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	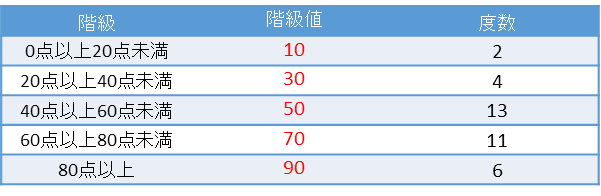データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	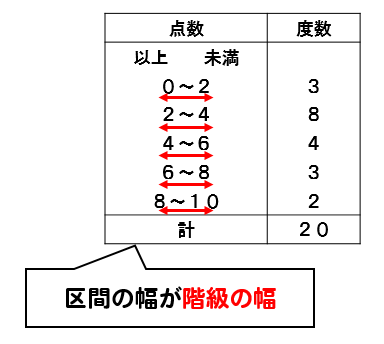データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	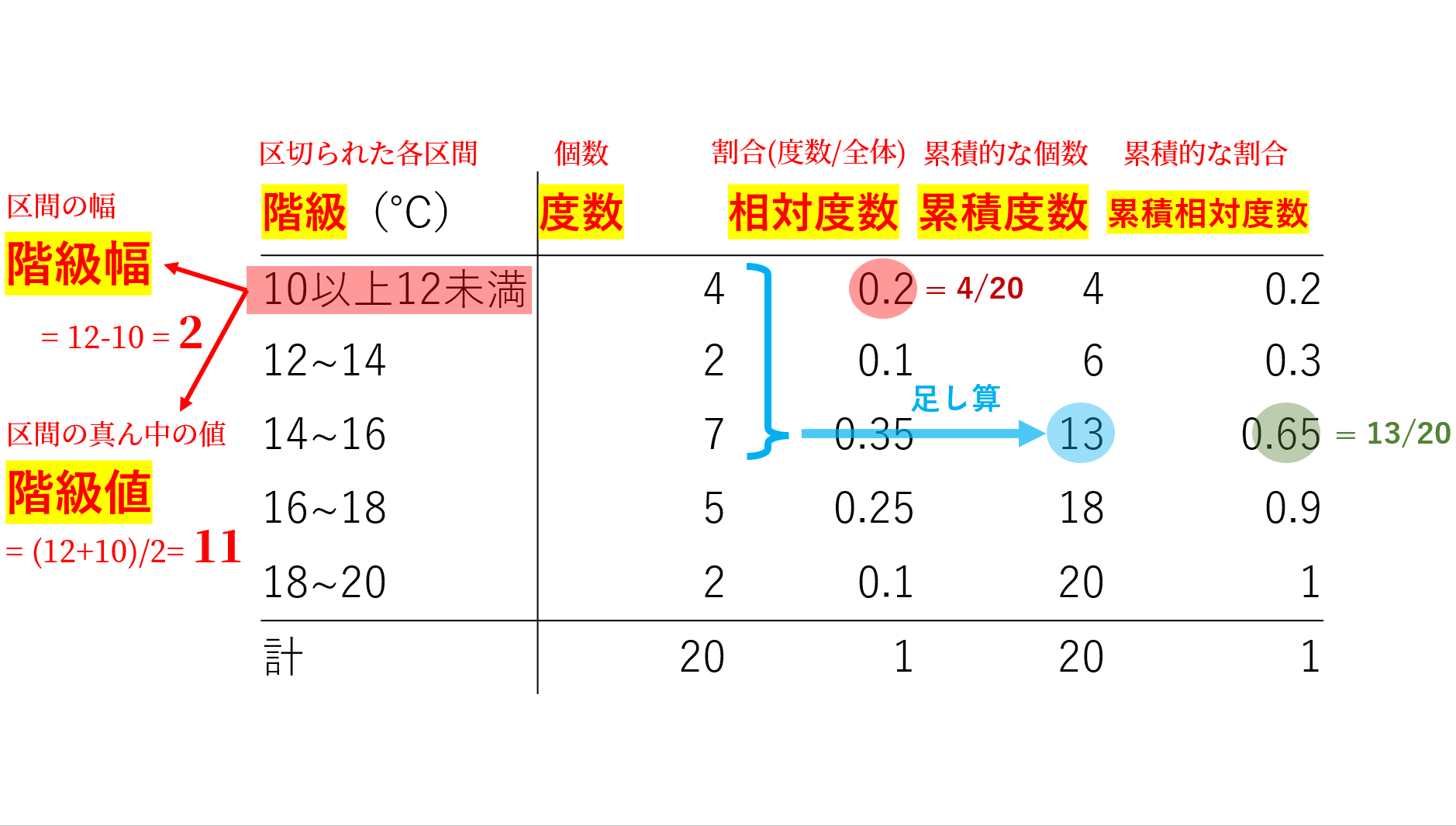データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	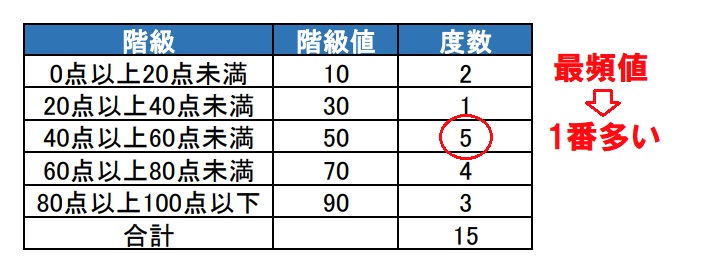データの平均値 中央値 最頻値の定義と解釈 数学の景色	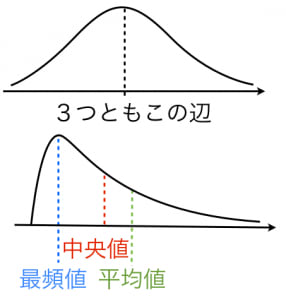データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色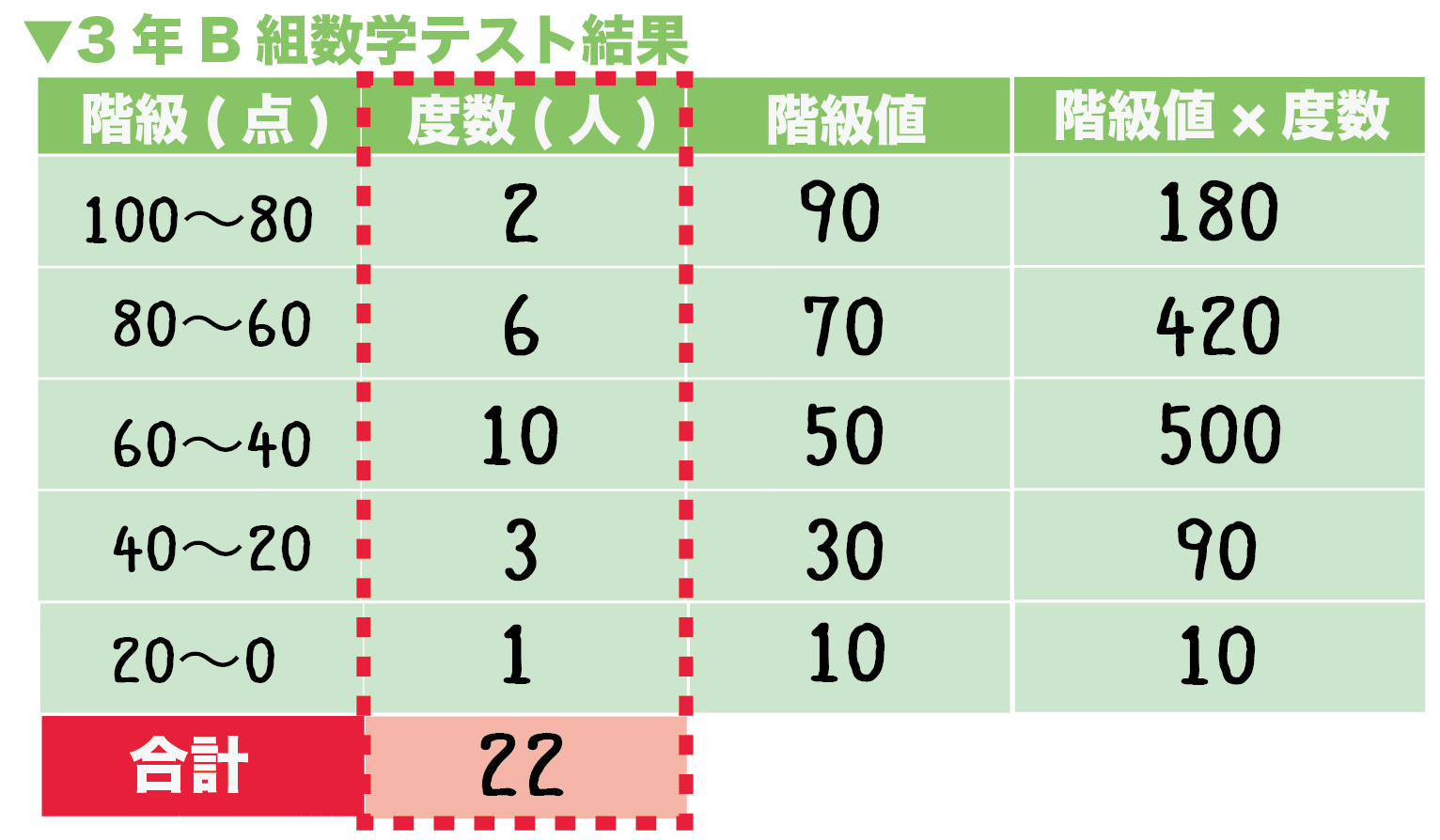
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	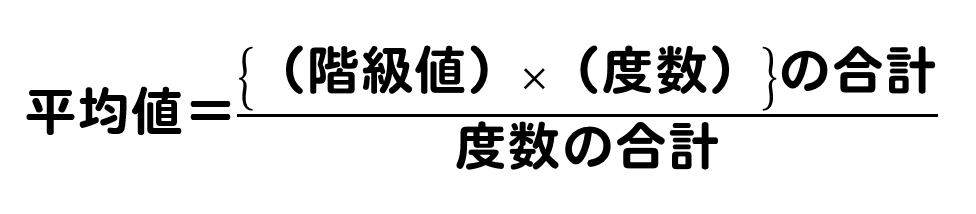データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色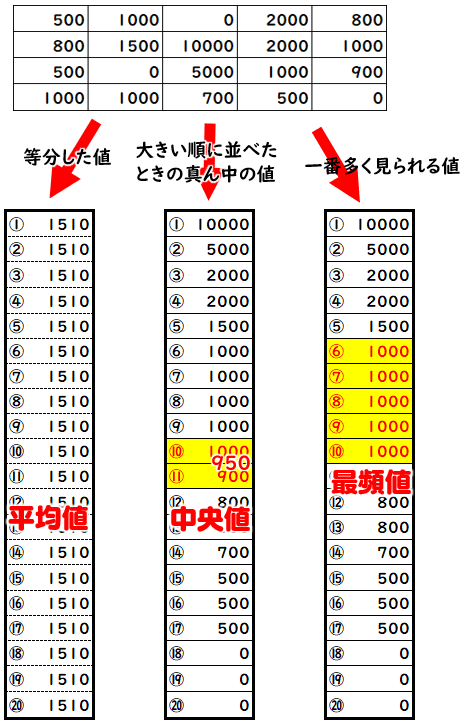
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色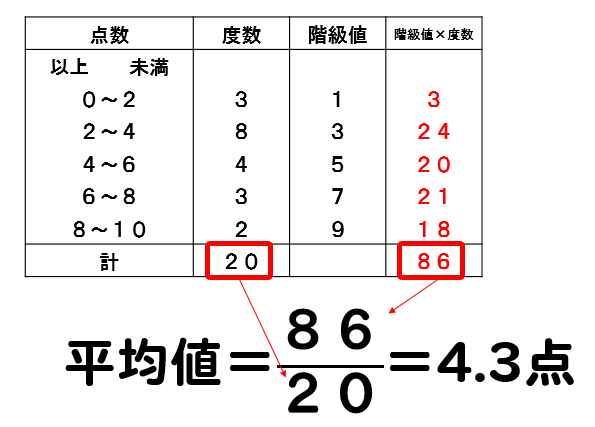
データの平均値 中央値 最頻値の定義と解釈 数学の景色	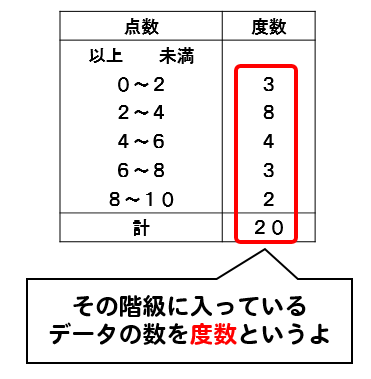データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	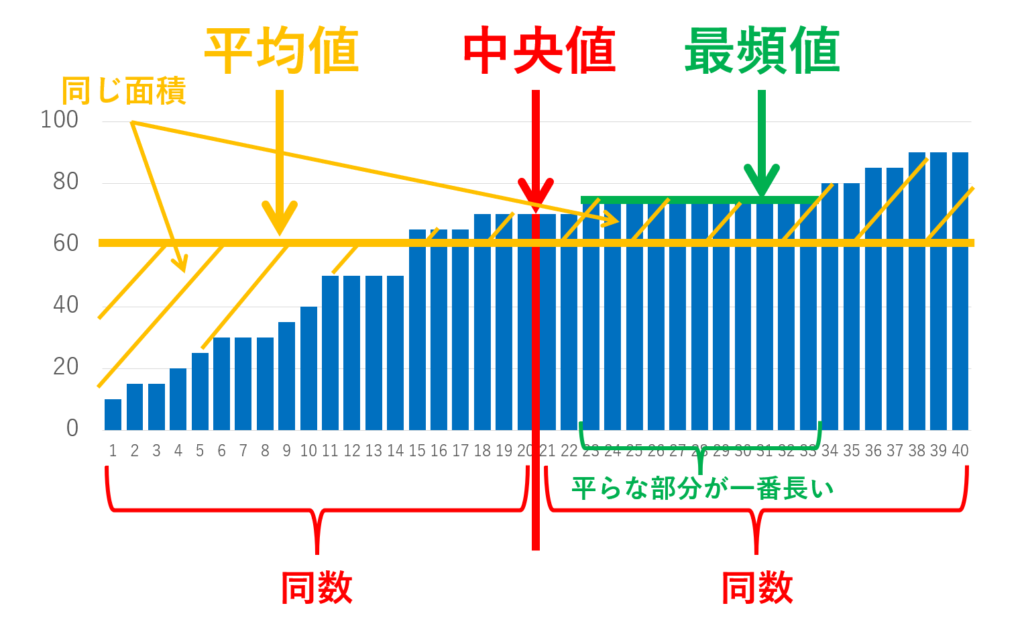データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色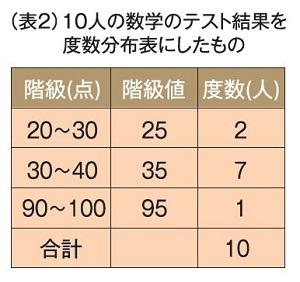
データの平均値 中央値 最頻値の定義と解釈 数学の景色	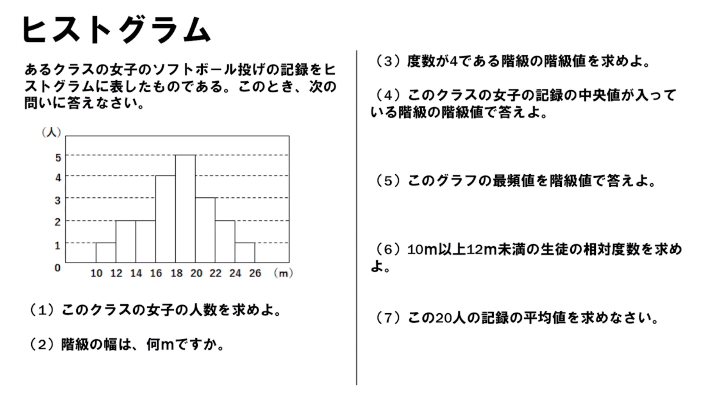データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	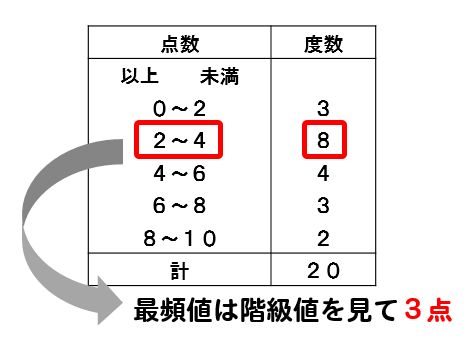データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	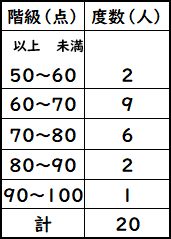データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	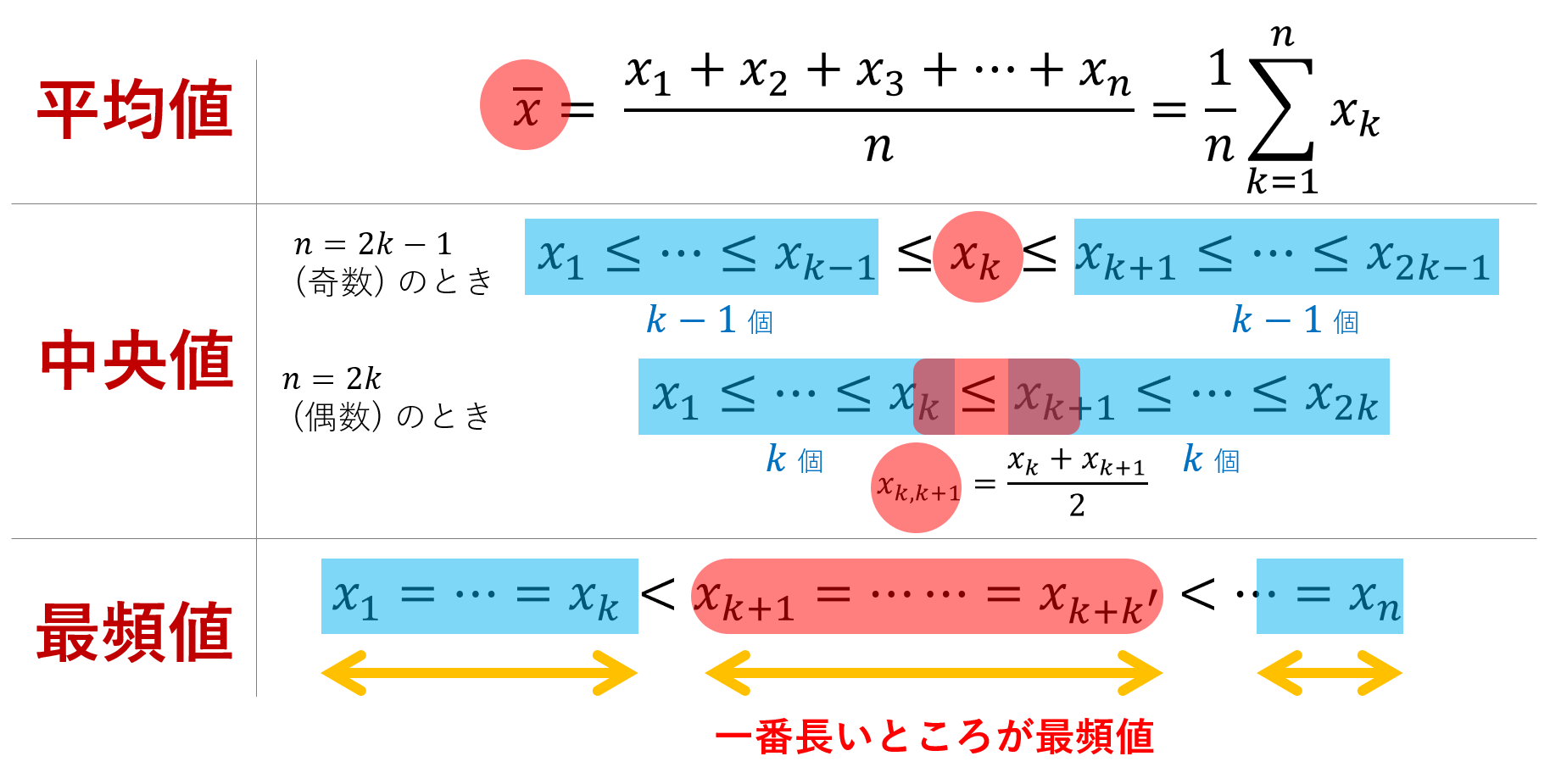データの平均値 中央値 最頻値の定義と解釈 数学の景色	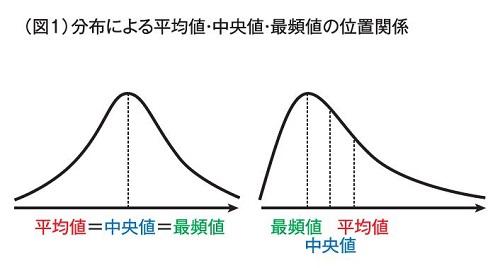データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	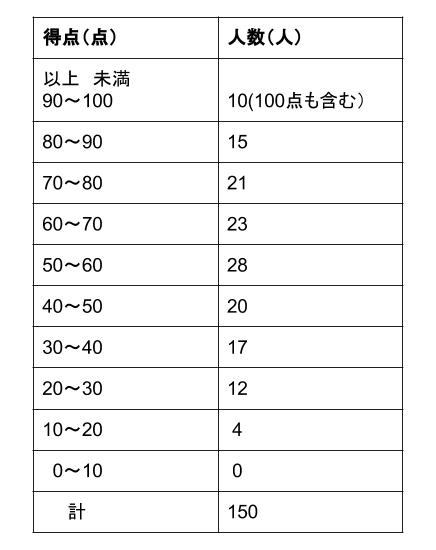データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	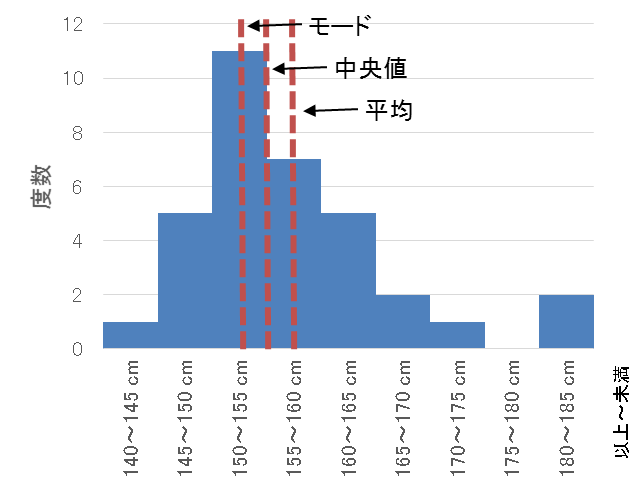データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	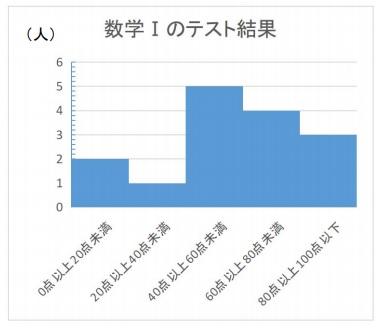データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	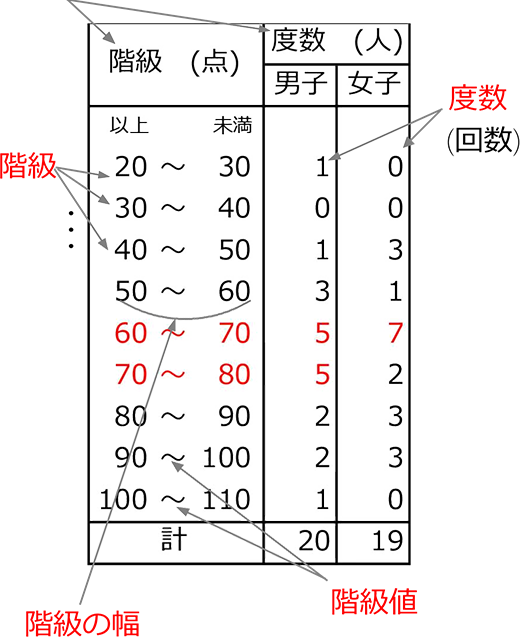データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色
データの平均値 中央値 最頻値の定義と解釈 数学の景色	データの平均値 中央値 最頻値の定義と解釈 数学の景色

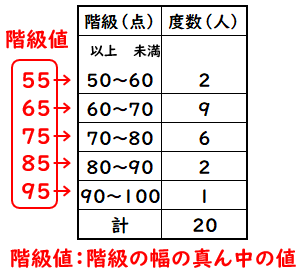
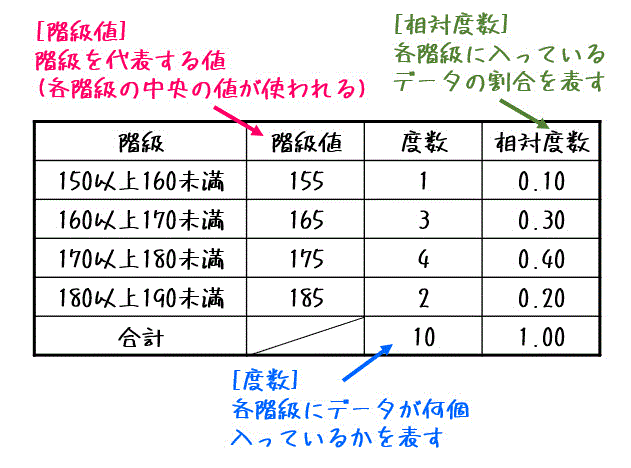
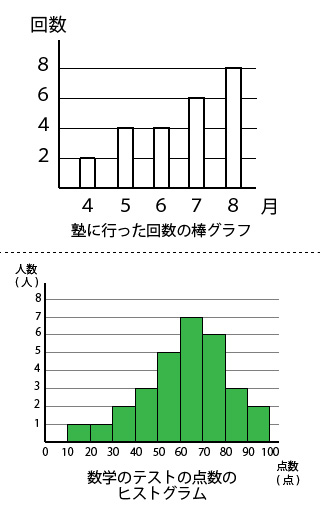
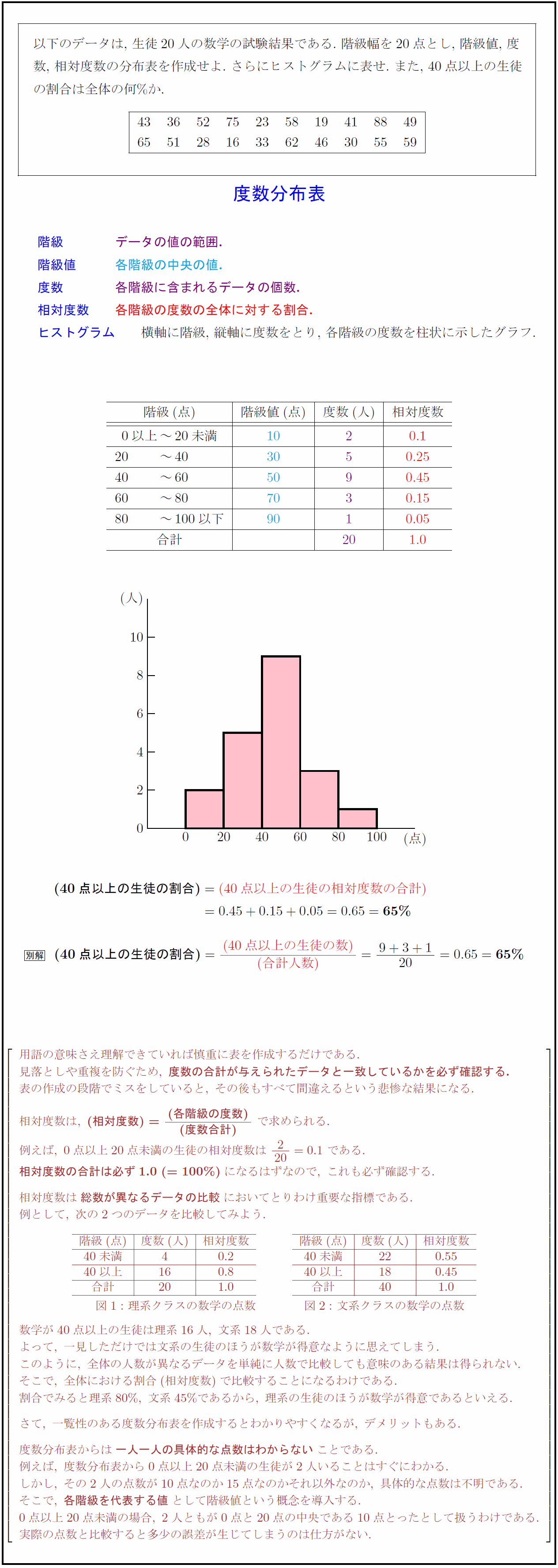
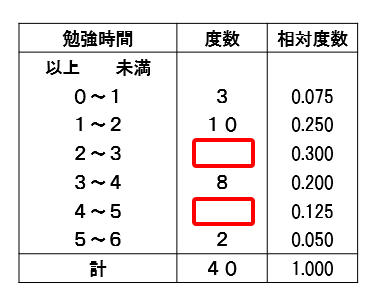
 度数分布表であれば 階級値・・・各階級の中央の値 例：階級が～25のときは225 求め方：その階級の最大と最小の値をたして2で割る さっきの例で言う (＋25)÷2 平均値・・・資料の特徴を1つの値で代表して表す 例：25 32 15 28の数字の平均値は25 求め方：資料の個々の値の合計を資料の個数で割る さっきの例で言う (25＋32＋15＋28)÷4 中央値・・・資料を資料を大きさの順 ヒストグラムでは、横軸に階級、縦軸に度数をとります。 階級 ：データを値の範囲で区切った つの区間（データ区間） 度数 ：各階級に属するデータの個数 そして、 つの階級がとる値の範囲を「 階級の幅 」、各階級の中央値を「 階級値 」といいます。 ヒストグラムを見ると、どのような範囲にデータが多く分布するのか、データが密集している／ばらけているなど、 データの特徴を

Incoming Term: 中1 数学階級値,